Recherche quantitative originale – Utilisation des arbres de classification et de régression pour modéliser les données manquantes sur l’IMC, la taille et la masse corporelle chez les jeunes

Résumé

Introduction. Les données issues de mesures de l’indice de masse corporelle (IMC) autodéclarées par les jeunes comportent souvent de graves lacunes, ce qui peut avoir un effet important sur les résultats des recherches les utilisant. La première étape du traitement des données manquantes consiste à étudier leur niveau et leur structuration. Or les études antérieures qui ont analysé les données manquantes sur l’IMC chez les jeunes ont utilisé une régression logistique, une approche limitée dans sa capacité à discerner des sous-groupes ou à obtenir une hiérarchie dans l’importance des variables, des dimensions pourtant susceptibles de contribuer grandement à la compréhension de la structuration des données manquantes.

Méthodologie. Cette étude a utilisé des modèles d’arbre de classification et de régression (CART, pour « classification and regression tree ») stratifiés selon le sexe pour analyser les données manquantes sur la taille, la masse corporelle et l’IMC chez 74 501 jeunes participant à l’étude COMPASS 2018-2019 (une étude de cohorte prospective qui a porté sur les comportements de santé des jeunes canadiens), dans laquelle 31 % des données sur l’IMC étaient manquantes. Des variables telles que le régime alimentaire, le mouvement, les résultats scolaires, la santé mentale et l’utilisation de substances ont été étudiées afin de vérifier leurs associations avec les données manquantes sur la taille, la masse corporelle et l’IMC.

Résultats. D’après les modèles CART, le fait d’être à la fois plus jeune, de se sentir en surpoids, d’être moins actif physiquement et d’avoir une santé mentale moins bonne a produit des sous-groupes de filles et de garçons où il était très probable que des valeurs d’IMC soient manquantes. Les données manquantes sur l’IMC étaient moins probables chez les répondants de l’enquête plus âgés et ne se sentant pas en surpoids.

Conclusion. Si l’on se fie aux sous-groupes produits par les modèles CART, utiliser un échantillon au sein duquel les cas dont la valeur de l’IMC est manquante ont été supprimés conduirait à tenir davantage compte des jeunes en meilleure santé sur les plans physique, émotionnel et mental. Étant donné que les modèles CART sont aptes à discerner ces sous-groupes ainsi qu’à établir une hiérarchie dans l’importance des variables, ils constituent un outil précieux pour étudier la structuration des données manquantes et la manière appropriée de gérer ces dernières.

Mots-clés : données manquantes, arbres de décision, surpoids, obésité, adolescents

Introduction

Littérature sur les données manquantes relatives au surpoids et à l’obésité

Étant donné qu’ils font partie des prédicteurs les plus importants de maladies chroniques^{Note de bas de page 1}, le surpoids et l’obésité demeurent l’un des principaux problèmes de santé dans le monde. De nombreuses études qui portent sur le surpoids et l’obésité utilisent l’indice de masse corporelle (IMC) extrait de mesures autodéclarées de la taille et de la masse corporelle afin de fournir une mesure approximative de l’adiposité corporelle. Les mesures autodéclarées sont généralement moins précises que les mesures anthropomorphiques prises directement – les individus ont tendance à sous-estimer leur masse corporelle et à surestimer leur taille^{Note de bas de page 2Note de bas de page 3Note de bas de page 4Note de bas de page 5} –, mais l’autodéclaration est généralement davantage réalisable (logistiquement et financièrement) que les autres approches de surveillance de la population^{Note de bas de page 3Note de bas de page 4Note de bas de page 5} et ces mesures sont utiles dans des contextes appropriés, où les limites des données sont comprises.

Un problème méthodologique moins débattu est celui de l’absence de réponse (c.-à-d. l’existence de données manquantes) dans l’autodéclaration de la taille et de la masse corporelle. Chez les jeunes, qui constituent un groupe cible fondamental dans la littérature sur la prévention du surpoids et de l’obésité, une grande proportion (parfois plus de 50 %) des données autodéclarées sur la taille et la masse corporelle ont tendance à être manquantes^{Note de bas de page 6Note de bas de page 7}. Si les données sont manquantes de manière complètement aléatoire (MCAR, c’est-à-dire « missing completely at random »), la probabilité de données manquantes ne dépend ni de la valeur réelle hypothétique de la variable manquante (sa valeur si elle était déclarée), ni des covariables observées. Mais si les données sont manquantes aléatoirement (MAR, c’est-à-dire « missing at random ») ou manquantes par omission prévisible (NMAR, c’est-à-dire « not missing at random »), la probabilité d’obtenir des données manquantes dépend alors des covariables observées (pour « manquantes aléatoirement ») et de la valeur réelle hypothétique de la variable manquante (pour « manquantes par omission prévisible »). La suppression des cas pour lesquels des valeurs sont manquantes (une méthode appelée « analyse des cas complets ») est une approche problématique, en particulier pour les deux derniers mécanismes, car elle entraîne un biais statistique^{Note de bas de page 8}. Par exemple, si des données manquent aléatoirement parce qu’il est plus probable que les participants plus jeunes ont davantage tendance à négliger de fournir les données sur leur poids, l’échantillon sera biaisé et favorisera les participants plus âgés (et ensuite, logiquement, les répondants dont le poids est plus élevé, compte tenu des modèles de croissance de l’enfant).

Cette introduction d’un biais statistique résultant de la suppression de cas a également été prouvée par de nombreuses études de simulation et elle est particulièrement notable lorsqu’il existe une proportion importante de données manquantes par omission prévisible^{Note de bas de page 8Note de bas de page 9}. Malgré cela, l’analyse des cas complets reste l’approche la plus courante dans la littérature épidémiologique^{Note de bas de page 10Note de bas de page 11}. Le taux élevé de données manquantes sur la taille et la masse corporelle autodéclarées chez les jeunes soulève des préoccupations quant à la manière dont les méthodes tiennent compte les données manquantes et comment un mauvais traitement des données manquantes a une incidence sur les résultats de recherche ainsi que sur les recommandations concomitantes en matière de politiques et de programmes.

Des approches statistiques sont souvent nécessaires pour le traitement des données manquantes. Or, alors que les chercheurs doivent suivre les pratiques exemplaires en matière de conception d’enquêtes, dans de nombreux cas, ils ne peuvent pas faire grand-chose pour améliorer les modèles de déclaration^{Note de bas de page 12Note de bas de page 13}. Bien qu’il existe des approches statistiques de pointe pour traiter de larges proportions de données manquantes par omission prévisible, elles nécessitent généralement plus de temps et d’expertise, ce qui peut constituer un obstacle à leur utilisation générale. Cela dit, une première étape importante vers la sélection d’une méthode raisonnable et pratique pour traiter les données manquantes consiste à comprendre l’étendue et la structuration des lacunes dans un ensemble de données. C’est important pour comprendre les sources potentielles des biais de non-déclaration, mais cela peut constituer également une étape importante pour déterminer les intrants dans certaines approches portant sur les données manquantes (comme l’imputation multiple). L’identification des diverses sources de données manquantes est particulièrement essentielle dans les grands ensembles de données comportant de nombreuses variables, dans la mesure où les méthodes de traitement des données manquantes peuvent facilement devenir exponentiellement compliquées. En outre, étant donné que les données manquantes sont généralement spécifiques à chaque étude, il n’existe pas de cadre clair portant sur les processus aptes à identifier des sources ou des mécanismes de lacune dans les données.

Approches de régression

Les recherches portant sur les données manquantes sur l’IMC ou la masse corporelle ont utilisé des approches de régression^{Note de bas de page 6Note de bas de page 7Note de bas de page 14}, où le résultat d’une régression logistique est « manquant » ou « non manquant » et où d’autres variables sont étudiées pour leur association potentielle avec la probabilité que les données soient manquantes. Les approches de régression ne sont pourtant pas toujours idéales dans cette situation, car la structuration des données manquantes peut être plus complexe que ce qu’offre une approche de régression simpliste. En outre, le processus de sélection des variables dans les modèles de régression peut être ambigu. Lors de la mise au point d’un modèle de régression, une première étape de sélection des variables pourrait consister à étudier la littérature portant sur des analyses similaires, mais celle-ci est rare dans le contexte de l’étude des données manquantes sur l’IMC.

Les comparaisons entre deux variables sont parfois aussi utilisées pour choisir les données de régression. Or, pour les ensembles de données volumineux dans lesquels les données manquantes sont substantielles, cette technique risque de ne pas être profitable pour l’élimination, car de nombreuses associations bivariées sont susceptibles d’être statistiquement significatives. On peut utiliser des procédures courantes de sélection de modèles telles que le critère d’information d’Akaike ou le critère d’information bayésien pour sélectionner des variables, mais ces procédures peuvent se révéler en pratique difficiles : nous avons précédemment étudié les données manquantes sur l’IMC, la taille et la masse corporelle à l’aide de procédures de sélection de modèles pour des modèles linéaires généralisés à effets mixtes^{Note de bas de page 15}, mais cela a nécessité de nombreuses décisions de modélisation supplémentaires et un algorithme personnalisé adapté aux méthodes de pseudo-vraisemblance^{Note de bas de page 16}.

Enfin, lorsque les processus de sélection des variables conduisent à un grand nombre de variables pertinentes, le processus de décision sur ce qu’il faut exclure pour produire un modèle parcimonieux peut ne pas être clair. Dans de tels cas, obtenir une hiérarchie dans l’importance des variables serait bénéfique car cela est susceptible de contribuer à la parcimonie et à une interprétation plus claire et cela peut constituer une étape nécessaire dans l’utilisation de certaines méthodes de traitement des données manquantes comme l’imputation multiple. Bien que notre étude précédente soit venue enrichir la littérature relative aux données manquantes sur l’IMC chez les jeunes, nous n’avons pas été en mesure de déterminer les variables les plus importantes ou les combinaisons de facteurs rendant l’absence de réponse plus probable^{Note de bas de page 15}. Or les limites associées à une approche de régression pour l’étude des données manquantes peuvent être dépassées grâce à une approche méthodologique différente.

Arbres de décision

Les arbres de décision sont un type d’approche par apprentissage automatique utilisée dans la recherche appliquée, notamment en santé publique^{Note de bas de page 17Note de bas de page 18}. Les arbres de décision sont utiles pour analyser les données primaires et pour étudier les données manquantes et ils peuvent également offrir une solution à certains des problèmes de sélection des variables décrits plus haut. Ils effectuent un partitionnement récursif des données par variables prédictives et peuvent traiter assez facilement de vastes ensembles de données comportant de multiples variables prédictives mesurées sur différentes échelles. Une fois élagués, les arbres de décision offrent une sélection déjà analysée des variables prédictives dans un format hiérarchique, ce qui permet une inférence sur l’importance de chaque variable. En outre, les arbres de décision permettent de faire émerger des sous-groupes importants et très spécifiques au-delà de ce qui est faisable en utilisant les termes d’interaction d’un modèle de régression.

De plus, contrairement à la régression, l’ensemble du modèle de l’arbre de décision peut être aisément visualisé, ce qui peut faciliter l’interprétation. En 2015, Tierney et al.^{Note de bas de page 19} ont publié un travail faisant la preuve de l’utilité des arbres de décision pour l’analyse des données manquantes mais, à notre connaissance, aucune étude publiée depuis n’a exploité cette approche.

L’objectif de cette étude est 1) d’enrichir le peu de littérature dont on dispose à propos des données manquantes sur la taille et sur la masse corporelle autodéclarées par les jeunes, 2) d’identifier les secteurs potentiels de biais découlant de la non-réponse dans le domaine du surpoids et de l’obésité chez les jeunes et 3) de monter comment utiliser les arbres de décision pour modéliser les données manquantes, en nous basant sur les travaux de Tierney et al.^{Note de bas de page 19}, qui sont les premiers à avoir fait la preuve de l’utilité de cette approche.

Méthodologie

Échantillon

Cette étude fait appel à un vaste ensemble de données transversales provenant de la vague 2018-2019 de l’étude COMPASS (« Cannabis, Obesity, Mental health, Physical activity, Alcohol, Smoking, Sedentary behaviour », c'est-à-dire cannabis, obésité, santé mentale, activité physique, alcool, tabagisme, comportements sédentaires), une étude de cohorte prospective qui recueille des données sur divers comportements de santé auprès des jeunes. Au cours de la vague 2018‑2019, on a recueilli des données auprès de 74 501 jeunes, soit un taux de participation de 84,3 %. L’étude COMPASS utilise un protocole d’information active et de consentement passif qui induit des taux de participation élevés. L’absence de participation est généralement attribuable à l’absentéisme ou aux périodes libres dans l’emploi du temps au moment de la collecte des données.

Variables

Cette étude cible les valeurs d’IMC manquantes ainsi que les valeurs de taille et de masse corporelle nécessaires pour le calcul de l’IMC. Des indicateurs binaires ont été créés pour chacune de ces variables afin d’indiquer si elles étaient manquantes ou non. La mesure de la masse corporelle repose sur les réponses à la question posée aux étudiants : « Combien pesez-vous sans vos chaussures? (Veuillez fournir votre réponse en livres OU en kilogrammes, puis indiquer la valeur correspondant à votre poids.) ». De manière similaire, la mesure de la taille a été obtenue en réponse à la question « Combien mesurez-vous sans vos chaussures? (Veuillez fournir votre taille en pieds et pouces OU en centimètres, puis indiquer la valeur correspondant à votre taille.) ». L’IMC se calcule en divisant la masse corporelle (kg) par la taille au carré (m²).

Les approches reposant sur un arbre de décision ont l’avantage de pouvoir inclure de nombreuses variables. Dans cette étude, nous avons inclus un large éventail de variables sur le régime alimentaire, le mouvement, les résultats scolaires, la santé mentale et l’utilisation de substances. Les variables liées au régime alimentaire étaient le nombre de portions de fruits et légumes, de produits céréaliers, de viande et substituts, de lait et substituts ainsi que le nombre de jours par semaine où les répondants prenaient un déjeuner, consommaient des boissons énergisantes et consommaient des aliments prêts-à-manger. Les variables liées au mouvement étaient l’activité physique modérée à vigoureuse, la pratique d’un sport (à l’école ou à l’extérieur de l’école), la musculation, des amis physiquement actifs, le temps d’écran sédentaire et le sommeil.

Les variables liées aux résultats scolaires étaient la note en anglais (ou la note en français, pour les écoles de langue française), la note en mathématiques et l’absentéisme. Les variables liées à la santé mentale étaient les symptômes cliniquement pertinents de la dépression (échelle CESD-R-10^{Note de bas de page 20}), l’anxiété (échelle GAD-7^{Note de bas de page 21}), la régulation émotionnelle (échelle DERS^{Note de bas de page 22}), le bien-être autodéclaré (échelle d’épanouissement psychologique^{Note de bas de page 23}), l’image de soi (forme abrégée du questionnaire II sur l’autodescription^{Note de bas de page 24}), la santé mentale autoévaluée et la mention autodéclarée de victime ou d’auteur d’intimidation. Les variables liées à l’utilisation de substances étaient la consommation occasionnelle excessive d’alcool, le tabagisme, l’utilisation de cigarettes électroniques, la consommation de cannabis et la consommation d’alcool mélangé à des boissons énergisantes. Bien que toutes ces variables aient été entrées dans les analyses, seul un sous-ensemble d’entre elles a émergé dans les modèles finaux.

Valeurs aberrantes

Dans certains cas, des valeurs manquantes ont été imposées aux données. Nous avons utilisé la règle de 1,5 fois l’écart interquartile pour repérer les valeurs statistiquement aberrantes, et ces valeurs limites ont été prises en compte parallèlement à la plausibilité biologique afin de déterminer comment traiter ces cas. Nous avons ainsi considéré comme poids manquants les poids inférieurs à 45 lb (20 kg) ou supérieurs à 390 lb (177 kg) et comme tailles manquantes les tailles inférieures à 4 pieds (1,22 m) ou supérieures à 6 pieds 11 pouces (2,11 m). Le sommeil et le temps d’écran sédentaire sont deux variables qui présentaient un certain nombre de valeurs aberrantes irréalisables dans l’ensemble de données. Les jeunes qui ont déclaré dormir régulièrement moins de 4 heures par nuit ou avoir un temps d’écran sédentaire total supérieur à 16,25 heures par jour ont été considérés comme ayant des données manquantes. Il convient de noter que les données manquantes ont été imposées uniquement pour la variable aberrante : par exemple, le sommeil a été considéré comme donnée manquante pour ceux qui avaient déclaré dormir moins de 4 heures par nuit, mais toutes les autres variables les concernant sont demeurées les mêmes.

Analyses

Dans cette étude, nous avons utilisé l’approche des arbres de classification et de régression (CART) où le résultat est binaire (manquant ou non manquant). Tous les modèles ont été stratifiés selon le sexe (féminin, masculin), qui était autodéclaré. Conformément aux approches en matière d’arbre de décision^{Note de bas de page 25}, les données ont été réparties en un ensemble de données de formation et un ensemble de données de test, comprenant respectivement 80 % et 20 % des données. L’ensemble des données de formation a été utilisé pour ajuster l’arbre, tandis que celui des données de test a été utilisé pour évaluer la précision prédictive de l’arbre de formation.

Nous avons utilisé l’élagage de complexité des coûts parallèlement à la règle d’une erreur-type (1 – ET)^{Note de bas de page 25} pour corriger le surajustement et produire un arbre final plus parcimonieux. Les analyses de l’arbre de décision ont été effectuées dans le progiciel statistique R (R Foundation for Statistical Computing, Vienne, Autriche) à l’aide du produit-programme rpart et les arbres élagués finaux ont été produits graphiquement à l’aide du produit-programme rattle. Nous avons formulé une restriction de pré-élagage de manière à ce que les nœuds finaux contiennent un nombre minimum d’individus. On a utilisé un nombre minimum d’individus dans une école pour chaque échantillon stratifié afin de déterminer ces seuils : 14 pour les filles et 16 pour les garçons. Les modèles ont inclus des individus ayant des covariables manquantes car le CART traite facilement cette situation au moyen du partitionnement de substitution : si la valeur d’une covariable est manquante, il utilise à la place la variable observée ayant la capacité prédictive la plus similaire.

Résultats

Statistiques descriptives

Le tableau 1 présente des statistiques descriptives stratifiées pour toute variable apparaissant dans au moins un des modèles CART. Sur l’ensemble de l’échantillon (n = 74 501), les valeurs de l’IMC étaient manquantes dans 31 % des cas. Les données manquantes sur la taille étaient légèrement plus fréquentes chez les garçons (19 %) que chez les filles (15 %) tandis que les données manquantes sur la masse corporelle étaient légèrement plus fréquentes chez les filles (22 %) que chez les garçons (20 %).

Tableau 1. Statistiques descriptives de l’échantillon de l’étude COMPASS, 2018-2019 (n = 74 501)

VariablesNote de bas de page a	Filles (n = 36 546)	Garçons (n = 37 126)	TotalNote de bas de page b (n = 74 501)
Variables liées à l’IMC
IMCNote de bas de page c moyen (valeur, ET)	20,98 (3,02)	21,21 (3,24)	21,10 (3,14)
Valeurs manquantes (%, n)	30,35 (11 093)	31,22 (11 591)	31,31 (23 329)
Taille moyenne (en m) (ET)	163,4 (7,50)	174,2 (10,24)	168,7 (10,47)
Données manquantes (%, n)	14,88 (5 439)	19,04 (7 067)	17,52 (13 049)
Masse corporelle moyenne (en kg) (ET)	57,42 (13,13)	66,59 (17,74)	62,16 (16,44)
Données manquantes (%, n)	21,75 (7 948)	19,79 (7 348)	21,33 (15 894)
Âge
Âge moyen (en années) (ET)	15,14 (1,50)	15,18 (1,51)	15,16 (1,51)
Données manquantes (%, n)	0,08 (31)	0,19 (69)	0,73 (541)
Origine ethniqueNote de bas de page d
Racisé (%, n)	69,45 (25 383)	68,62 (25 477)	68,48 (51 017)
Non racisé (%, n)	30,27 (11 063)	30,99 (11 505)	30,63 (22 822)
Données manquantes (%, n)	0,27 (100)	0,39 (144)	0,89 (662)
Perception du poids
Poids insuffisant (%, n)	11,47 (4 190)	21,00 (7 795)	16,30 (12 140)
Poids excessif (%, n)	25,85 (9 448)	19,93 (7 398)	22,87 (17 038)
Poids à peu près juste (%, n)	61,14 (22 343)	57,19 (21 233)	58,92 (43 893)
Données manquantes (%, n)	1,55 (565)	1,89 (700)	1,92 (1 430)
Variables liées au régime alimentaire
Consommation de fruits et légumes (rappel de 24 heures)
Nombre moyen de portions (n, ET)	2,89 (1,89)	3,06 (2,11)	2,98 (2,01)
Données manquantes (%, n)	2,44 (890)	4,74 (1 759)	3,79 (2 822)
Consommation de viande et substituts de la viande (rappel de 24 heures)
Nombre moyen de portions (n, ET)	1,88 (1,03)	2,41 (1,20)	2,15 (1,15)
Données manquantes (%, n)	2,45 (896)	4,76 (1 766)	3,80 (2 833)
Déjeuner le matin
Nombre moyen de jours par semaine (n, ET)	4,67 (2,37)	5,05 (2,33)	4,85 (2,36)
Données manquantes (%, n)	1,31 (479)	2,30 (855)	1,99 (1 484)
Consommation de produits céréaliers (rappel de 24 heures)
Nombre moyen de portions (n, ET)	2,41 (1,52)	2,98 (1,93)	2,69 (1,77)
Données manquantes (%, n)	2,33 (851)	4,61 (1 711)	3,67 (2 737)
Consommation de lait et substituts du lait (rappel de 24 heures)
Nombre moyen de portions (n, ET)	1,77 (1,32)	2,39 (1,54)	2,08 (1,47)
Données manquantes (%, n)	2,33 (853)	4,57 (1 697)	3,66 (2 724)
Consommation d’aliments prêts-à-manger
Nombre moyen de jours par semaine (n, ET)	1,19 (1,34)	1,43 (1,61)	1,31 (1,49)
Données manquantes (%, n)	1,03 (380)	2,16 (801)	1,81 (1 345)
Variables liées au mouvement
Pratique d’un sport
Ont fait du sport (%, n)	56,70 (20 720)	62,05 (23 036)	59,24 (44 135)
N’ont pas fait de sport (%, n)	41,70 (15 241)	35,25 (13 088)	38,41 (28 618)
Données manquantes (%, n)	1,60 (585)	2,70 (1 002)	2,35 (1 748)
Musculation
Nombre moyen de jours par semaine (n, ET)	2,24 (2,02)	2,77 (2,27)	2,51 (2,16)
Données manquantes (%, n)	1,29 (473)	1,93 (717)	1,80 (1 344)
Amis physiquement actifs
Nombre moyen (n, ET)	3,03 (1,68)	3,52 (1,69)	3,28 (1,71)
Données manquantes (%, n)	1,35 (494)	2,13 (789)	1,92 (1 430)
Temps d’écran sédentaire
Nombre moyen d’heures par jour (n, ET)	5,92 (3,35)	6,37 (3,37)	6,15 (3,37)
Données manquantes (%, n)	4,41 (1 613)	5,94 (2 206)	5,44 (4 056)
Activité physique modérée à vigoureuse
Nombre moyen d’heures par jour (n, ET)	1,60 (1,23)	2,00 (1,47)	1,80 (1,38)
Données manquantes (%, n)	1,87 (683)	2,56 (949)	2,39 (1 777)
Sommeil
Moyenne d’heures par nuit (n, ET)	7,47 (1,30)	7,60 (1,28)	7,54 (1,29)
Données manquantes (%, n)	7,33 (2 679)	8,92 (3 310)	8,38 (6 241)
Variables liées aux résultats scolaires
Note en anglais (ou en français, dans le cas d’écoles de langue française)
Note < 50 % (%, n)	1,09 (399)	2,44 (907)	1,83 (1 362)
Note ≥ 50 % (%, n)	95,39 (34 862)	91,92 (34 128)	93,41 (69 590)
Données manquantes (%, n)	3,52 (1 285)	5,63 (2 091)	4,76 (3 549)
Variables liées à la santé mentale
Santé mentale autoévaluée
Score moyen (ET)	2,76 (1,21)	2,21 (1,15)	2,49 (1,21)
Données manquantes (%, n)	3,37 (1 230)	6,05 (2 245)	4,93 (3 670)
Bien-êtreNote de bas de page e
Score moyen (ET)	31,78 (5,75)	32,64 (5,60)	32,19 (5,72)
Données manquantes (%, n)	4,84 (1 770)	6,78 (2 518)	6,02 (4 486)
Image de soiNote de bas de page f
Score moyen (ET)	11,79 (4,69)	9,76 (4,19)	10,79 (4,58)
Données manquantes (%, n)	3,34 (1 221)	5,51 (2 045)	4,64 (3 455)
Variables liées à l’utilisation de substances
Tabagisme
Au cours des 30 derniers jours (%, n)	6,64 (2 425)	8,00 (2 969)	7,43 (5 532)
Pas au cours des 30 derniers jours (%, n)	92,89 (33 949)	91,01 (33 790)	91,70 (68 320)
Données manquantes (%, n)	0,47 (172)	0,99 (367)	0,87 (649)
Utilisation de cigarettes électroniques
Au cours des 30 derniers jours (%, n)	25,48 (9 312)	30,34 (11 264)	27,99 (20 852)
Pas au cours des 30 derniers jours (%, n)	73,75 (26 951)	67,98 (25 237)	70,62 (52 614)
Données manquantes (%, n)	0,77 (172)	1,68 (625)	1,39 (1 035)
Consommation de cannabis
Au cours des 30 derniers jours (%, n)	10,95 (4 001)	14,70 (5 458)	12,97 (9 662)
Pas au cours des 30 derniers jours (%, n)	88,06 (32 183)	83,36 (30 950)	85,42 (63 637)
Données manquantes (%, n)	1,00 (362)	2,32 (718)	1,61 (1 202)

Interprétation des modèles CART

Les résultats stratifiés selon le sexe des modèles CART sont présentés dans les figures 1 à 3. La figure 1 fournit les résultats pour les données manquantes sur l’IMC, la figure 2 pour les données manquantes sur la masse corporelle et la figure 3 pour les données manquantes sur la taille. Tous les modèles CART peuvent se lire à partir du nœud racine (nœud 1) en haut de l’arborescence, qui contient toutes les données de formation pour l’ensemble de données dont il est question. Les nœuds sous le nœud 1 correspondent aux partitions de l’arbre, une partition à gauche signifiant toujours un « oui » et une partition à droite toujours un « non », et ce, pour les variables continues comme pour les variables catégorielles. L’étiquette et la couleur de chaque nœud, « présence » (en vert) ou « absence » (en bleu), correspondent à la situation la plus probable pour les données de ce nœud. Les nuances de couleur précisent les probabilités (les couleurs plus foncées indiquant une plus forte probabilité) et les probabilités sont également mentionnées dans chaque nœud, sur le côté gauche pour la probabilité de présence et sur le côté droit pour la probabilité d’absence. Les variables qui apparaissent plus haut dans l’arborescence (plus près du nœud 1) et celles qui apparaissent plus souvent peuvent être considérées comme des critères plus pertinents que les variables qui apparaissent uniquement plus bas dans l’arbre.

Par exemple, dans le modèle CART des données manquantes sur l’IMC des filles (figure 1), les données sont d’abord divisées selon la perception du poids. Si les répondantes dans cet échantillon ont perçu leur poids comme étant « à peu près juste » ou « insuffisant », elles sont dans le nœud 2. Le nœud 2 contient 74 % de l’échantillon et, dans ce nœud, la probabilité que les valeurs de l’IMC soient manquantes est de 0,27. Si les répondantes ont perçu leur poids comme « excessif » (l’autre catégorie restante pour cette variable), elles seront dans le nœud 3, qui contient 26 % des données et où la probabilité que les valeurs de l’IMC soient manquantes est de 0,38. De même, pour les variables continues, les modèles CART identifient des seuils. Par exemple, dans le modèle des données manquantes sur l’IMC des filles, le deuxième nœud indique que le modèle a estimé que l’âge de 15 ans était le seuil qui différenciait le plus les nœuds inférieurs suivants.

Figure 1 - Équivalent textuel

La figure 1 comprend deux figures plus petites : une pour les femmes et une pour les hommes. Chaque figure est un ensemble de nœuds avec des données. Les nœuds sont rangés de manière binaire selon certaines catégories.

La description textuelle suivante présente les données pour les femmes, suivies de celles pour les hommes. Chaque figure nécessite trois tableaux pour sa description textuelle.

Figure 1 – Femmes – Équivalent textuel Tableau 1

Noeud	Étiquette et couleur de chaque noeud	Probabilité que les valeurs de l’IMC soient présentes	Probabilité que les valeurs de l’IMC soient manquantes	Pourcentage de l’échantillon	Catégorie dans laquelle le nœud peut être subdivisé	Nœuds qui suivent la subdivision pour « oui » et « non » respectivement
1	« présence » (en vert)	0,7	0,3	100 %	PERCEPTION DU POIDS = à peu près juste, poids insuffisant	2, 3
2	« présence » (en vert)	0,73	0,27	74 %	ÂGE ≥ 15	4, 5
3	« présence » (en vert)	0,62	0,38	26 %	MUSCULATION ≥ 0,5	6, 7
4	« présence » (en vert)	0,77	0,23	47 %	S.O.	S.O.
5	« présence » (en vert)	0,65	0,35	27 %	ÂGE ≥ 13	10, 11
6	« présence » (en vert)	0,65	0,35	18 %	S.O.	S.O.
7	« présence » (en vert)	0,55	0,45	8 %	ANGLAIS = Note de passage	14, 15
10	« présence » (en vert)	0,67	0,33	23 %	S.O.	S.O.
11	« présence » (en vert)	0,52	0,48	4 %	TABAGISME = Non-fumeur	22, 23
14	« présence » (en vert)	0,56	0,44	8 %	BIEN-ÊTRE ≥ 26	28, 29
15	« absence » (en bleu)	0,2	0,8	0 %	S.O.	S.O.
22	« présence » (en vert)	0,54	0,46	4 %	SOMMEIL ≥ 7,4	44, 45
23	« absence » (en bleu)	0,15	0,85	0 %	S.O.	S.O.
28	« présence » (en vert)	0,58	0,42	6 %	S.O.	S.O.
29	« absence » (en bleu)	0,49	0,51	2 %	SANTÉ MENTALE AUTOÉVALUÉE ≥ 2,5	58, 59
44	« présence » (en vert)	0,56	0,44	3 %	S.O.	S.O.
45	« absence » (en bleu)	0,38	0,62	1 %	S.O.	S.O.
58	« présence » (en vert)	0,51	0,49	2 %	AMIS PHYSIQUEMENT ACTIFS ≥ 1,5	116, 117
59	« absence » (en bleu)	0,12	0,88	0 %	S.O.	S.O.
116	« présence » (en vert)	0,57	0,43	1 %	S.O.	S.O.
117	« absence » (en bleu)	0,45	0,55	1 %	S.O.	S.O.

Le tableau suivant décrit les variables binaires de chacun des nœuds du tableau précédent. « Oui » signifie que le nœud inclut cette catégorie ; « non » indique l'autre catégorie restante. « S.O. » signifie que le nœud n'est pas atteint par cette catégorie en tant que nœud parent (par exemple, parce qu'il s'agit du nœud racine, ou parce qu’il est le nœud le plus éloigné du nœud racine, ou parce qu'il se trouve dans une autre région du modèle, etc.)

Figure 1 – Femmes – Équivalent textuel tableau 2

Noeud	PERCEPTION DU POIDS = à peu près juste, poids insuffisant	ÂGE ≥ 15	ÂGE ≥ 13	TABAGISME = Non-fumeur	SOMMEIL ≥ 7,4	MUSCULATION ≥ 0,5	ANGLAIS = Note de passage	BIEN-ÊTRE ≥ 26	SANTÉ MENTALE AUTOÉVALUÉE ≥ 2,5	AMIS PHYSIQUEMENT ACTIFS ≥ 1,5
1	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
2	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
3	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
4	Oui	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
5	Oui	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
6	Non	S.O.	S.O.	S.O.	S.O.	Oui	S.O.	S.O.	S.O.	S.O.
7	Non	S.O.	S.O.	S.O.	S.O.	Non	S.O.	S.O.	S.O.	S.O.
10	Oui	Non	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
11	Oui	Non	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
14	Non	S.O.	S.O.	S.O.	S.O.	Non	Oui	S.O.	S.O.	S.O.
15	Non	S.O.	S.O.	S.O.	S.O.	Non	Non	S.O.	S.O.	S.O.
22	Oui	Non	Non	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
23	Oui	Non	Non	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
28	Non	S.O.	S.O.	S.O.	S.O.	Non	Oui	Oui	S.O.	S.O.
29	Non	S.O.	S.O.	S.O.	S.O.	Non	Oui	Non	S.O.	S.O.
44	Oui	Non	Non	Oui	Oui	S.O.	S.O.	S.O.	S.O.	S.O.
45	Oui	Non	Non	Oui	Non	S.O.	S.O.	S.O.	S.O.	S.O.
58	Non	S.O.	S.O.	S.O.	S.O.	Non	Oui	Non	Oui	S.O.
59	Non	S.O.	S.O.	S.O.	S.O.	Non	Oui	Non	Non	S.O.
116	Non	S.O.	S.O.	S.O.	S.O.	Non	Oui	Non	Oui	Oui
117	Non	S.O.	S.O.	S.O.	S.O.	Non	Oui	Non	Oui	Non

Le tableau suivant décrit la distance entre chaque catégorie et le nœud racine. Par exemple, le nombre « 2 » signifierait que la catégorie est à deux branches du nœud racine (le nœud no. 1).

Figure 1 – Femmes – Équivalent textuel tableau 3

Nom de la catégorie (variable binaire)	Distance du nœud racine
PERCEPTION DU POIDS = à peu près juste, poids insuffisant	1
ÂGE ≥ 15	2
MUSCULATION ≥ 0,5	2
ÂGE ≥ 13	3
ANGLAIS = Nonte de passage	3
TABAGISME = Nonn-fumeur	4
BIEN-ÊTRE ≥ 26	4
SOMMEIL ≥ 7,4	5
SANTÉ MENTALE AUTOÉVALUÉE ≥ 2,5	5
AMIS PHYSIQUEMENT ACTIFS ≥ 1,5	6

Figure 1 – Hommes – Équivalent textuel tableau 1

Noeud	Étiquette et couleur de chaque noeud	Probabilité que les valeurs de l’IMC soient présentes	Probabilité que les valeurs de l’IMC soient manquantes	Pourcentage de l’échantillon	Catégorie dans laquelle le nœud peut être subdivisé	Nœuds qui suivent la subdivision pour « oui » et « non » respectivement
1	« présence » (en vert)	0,69	0,31	100 %	SPORTS = oui, pratique sportive	2, 3
2	« présence » (en vert)	0,74	0,26	64 %	S.O.	S.O.
3	« présence » (en vert)	0,59	0,41	36 %	PERCEPTION DU POIDS = à peu près juste, poids insuffisant	6, 7
6	« présence » (en vert)	0,63	0,37	26 %	ÂGE ≥ 16	12, 13
7	« absence » (en bleu)	0,47	0,53	9 %	HEURES D’ACTIVITÉ PHYSIQUE ≥ 0,41	14, 15
12	« présence » (en vert)	0,7	0,3	12 %	S.O.	S.O.
13	« présence » (en vert)	0,56	0,44	14 %	HEURES D’ACTIVITÉ PHYSIQUE ≥ 0,52	26, 27
14	« absence » (en bleu)	0,49	0,51	7 %	IMAGE DE SOI < 22	28, 29
15	« absence » (en bleu)	0,36	0,64	2 %	S.O.	S.O.
26	« présence » (en vert)	0,59	0,41	11 %	ÂGE ≥ 15	52, 53
27	« absence » (en bleu)	0,47	0,53	3 %	ÂGE ≥ 13	54, 55
28	« présence » (en vert)	0,5	0,5	7 %	TEMPS D’ÉCRAN SÉDENTAIRE < 5,9	56, 57
29	« absence » (en bleu)	0,25	0,75	0 %	S.O.	S.O.
52	« présence » (en vert)	0,65	0,35	5 %	S.O.	S.O.
53	« présence » (en vert)	0,55	0,45	6 %	FRUITS ET LÉGUMES ≥ 1,5	106, 107
54	« absence » (en bleu)	0,49	0,51	3 %	ECIG = oui, utilisation de la cigarette électronique	108, 109
55	« absence » (en bleu)	0,25	0,75	0 %	S.O.	S.O.
56	« présence » (en vert)	0,57	0,43	3 %	PETIT-DÉJEUNER ≥ 1,5	112, 113
57	« absence » (en bleu)	0,46	0,54	5 %	PRODUITS CÉRÉALIERS< 8,5	114, 115
106	« présence » (en vert)	0,59	0,41	4 %	S.O.	S.O.
107	« absence » (en bleu)	0,46	0,54	2 %	S.O.	S.O.
108	« présence » (en vert)	0,6	0,4	1 %	S.O.	S.O.
109	« absence » (en bleu)	0,46	0,54	2 %	FRUITS ET LÉGUMES ≥ 3,5	218, 219
112	« présence » (en vert)	0,6	0,4	2 %	S.O.	S.O.
113	« absence » (en bleu)	0,41	0,59	0 %	S.O.	S.O.
114	« absence » (en bleu)	0,47	0,53	4 %	ECIG = oui, utilisation de la cigarette électronique	228, 229
115	« absence » (en bleu)	0,19	0,81	0 %	S.O.	S.O.
218	« présence » (en vert)	0,6	0,4	1 %	S.O.	S.O.
219	« absence » (en bleu)	0,42	0,58	2 %	S.O.	S.O.
228	« présence » (en vert)	0,54	0,46	1 %	S.O.	S.O.
229	« absence » (en bleu)	0,44	0,56	3 %	S.O.	S.O.

Le tableau suivant décrit les variables binaires de chacun des nœuds du tableau précédent. « Oui » signifie que le nœud inclut cette catégorie ; « non » indique l'autre catégorie restante. « S.O. » signifie que le nœud n'est pas atteint par cette catégorie en tant que nœud parent (par exemple, parce qu'il s'agit du nœud racine, ou parce qu’il est le nœud le plus éloigné du nœud racine, ou parce qu'il se trouve dans une autre région du modèle, etc.)

Figure 1 – Hommes – Équivalent textuel tableau 2

Noeud	SPORTS = oui, pratique sportive	PERCEPTION DU POIDS = à peu près juste, poids insuffisant	ÂGE ≥ 16	HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.41	HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.52	IMAGE DE SOI < 22	ÂGE ≥ 15	ÂGE ≥ 13	TEMPS D’ÉCRAN SÉDENTAIRE < 5.9	FRUITS ET LÉGUMES ≥ 1.5	ECIG = oui, utilisation de la cigarette électronique	PETIT-DÉJEUNER ≥ 1.5	PRODUITS CÉRÉALIERS< 8.5	FRUITS ET LÉGUMES ≥ 3.5	ECIG = oui, utilisation de la cigarette électronique
1	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
3	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
6	Non	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
7	Non	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
13	Non	Oui	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
14	Non	Non	S.O.	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
15	Non	Non	S.O.	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
26	Non	Oui	Non	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
27	Non	Oui	Non	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
28	Non	Non	S.O.	Oui	S.O.	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
53	Non	Oui	Non	Oui	S.O.	S.O.	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
54	Non	Oui	Non	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
56	Non	Non	S.O.	Oui	S.O.	Oui	S.O.	S.O.	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
57	Non	Non	S.O.	Oui	S.O.	Oui	S.O.	S.O.	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
109	Non	Oui	Non	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	Non	S.O.	S.O.	S.O.	S.O.
114	Non	Non	S.O.	Oui	S.O.	Oui	S.O.	S.O.	Non	S.O.	S.O.	S.O.	Oui	S.O.	S.O.
2	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
12	Non	Oui	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
52	Non	Oui	Non	Oui	S.O.	S.O.	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
106	Non	Oui	Non	Oui	S.O.	S.O.	Oui	S.O.	S.O.	Oui	S.O.	S.O.	S.O.	S.O.	S.O.
107	Non	Oui	Non	Oui	S.O.	S.O.	Oui	S.O.	S.O.	Non	S.O.	S.O.	S.O.	S.O.	S.O.
108	Non	Oui	Non	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	Oui	S.O.	S.O.	S.O.	S.O.
218	Non	Oui	Non	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	Non	S.O.	S.O.	Oui	S.O.
219	Non	Oui	Non	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	Non	S.O.	S.O.	Non	S.O.
55	Non	Oui	Non	Non	S.O.	S.O.	S.O.	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
112	Non	Non	S.O.	Oui	S.O.	Oui	S.O.	S.O.	Oui	S.O.	S.O.	Oui	S.O.	S.O.	S.O.
113	Non	Non	S.O.	Oui	S.O.	Oui	S.O.	S.O.	Oui	S.O.	S.O.	Non	S.O.	S.O.	S.O.
228	Non	Non	S.O.	Oui	S.O.	Oui	S.O.	S.O.	Non	S.O.	Oui	S.O.	Oui	S.O.	S.O.
229	Non	Non	S.O.	Oui	S.O.	Oui	S.O.	S.O.	Non	S.O.	Non	S.O.	Oui	S.O.	S.O.
115	Non	Non	S.O.	Oui	S.O.	Oui	S.O.	S.O.	Non	S.O.	S.O.	S.O.	Non	S.O.	S.O.
29	Non	Non	S.O.	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
15	Non	Non	S.O.	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.

Le tableau suivant décrit la distance entre chaque catégorie et le nœud racine. Par exemple, le nombre « 2 » signifierait que la catégorie est à deux branches du nœud racine (le nœud no. 1).

Figure 1 – Hommes – Équivalent textuel tableau 3

Nom de la catégorie (variable binaire)	Distance du nœud racine
SPORTS = oui, pratique sportive	1
PERCEPTION DU POIDS = à peu près juste, poids insuffisant	2
ÂGE ≥ 16	3
HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.41	3
HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.52	4
IMAGE DE SOI < 22	4
ÂGE ≥ 15	5
ÂGE ≥ 13	5
TEMPS D’ÉCRAN SÉDENTAIRE < 5.9	5
FRUITS ET LÉGUMES ≥ 1.5	6
ECIG = oui, utilisation de la cigarette électronique	6
PETIT-DÉJEUNER ≥ 1.5	6
PRODUITS CÉRÉALIERS< 8.5	6
FRUITS ET LÉGUMES ≥ 3.5	7
ECIG = oui, utilisation de la cigarette électronique	7

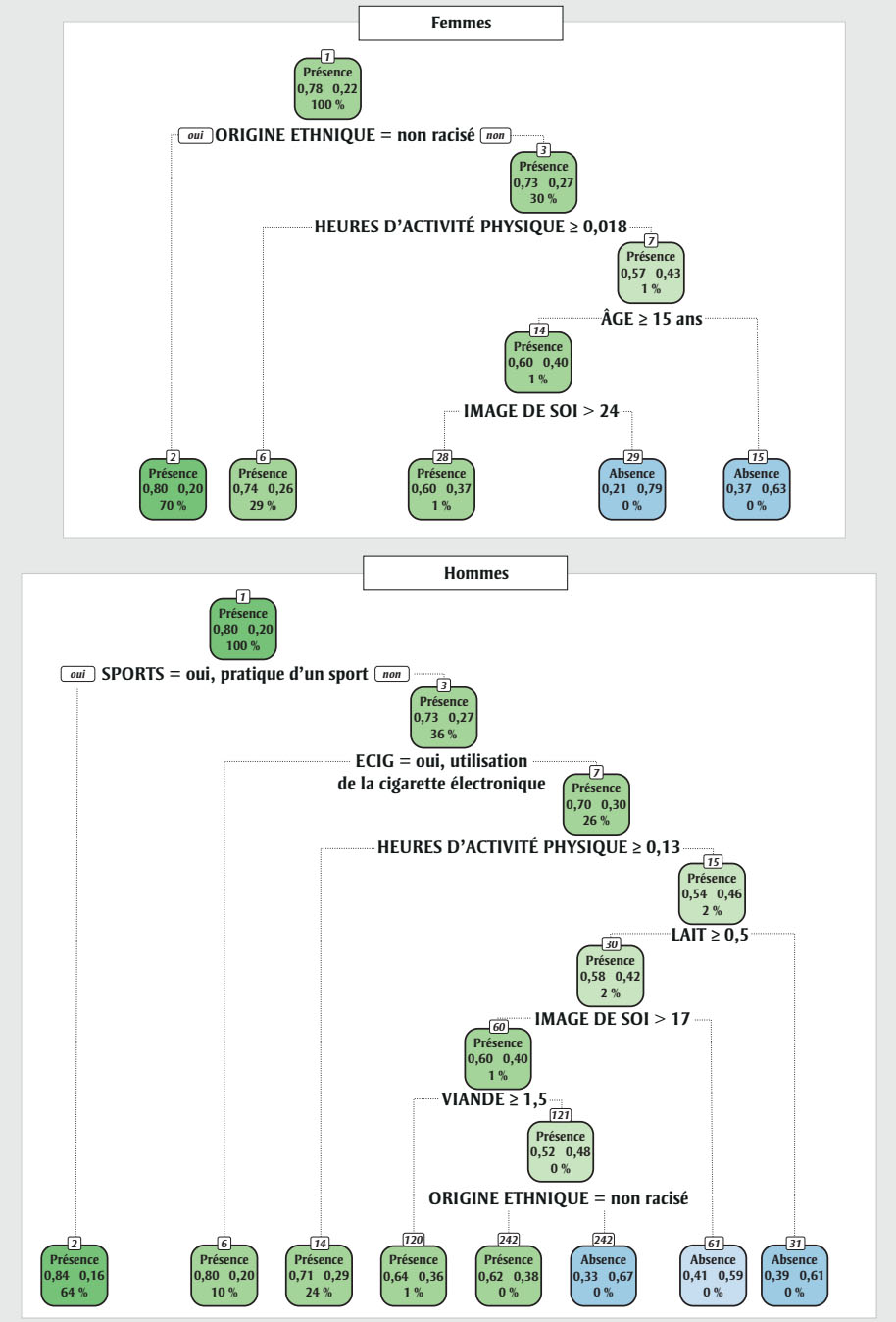
Figure 2 - Équivalent textuel

La figure 1 comprend deux figures plus petites : une pour les femmes et une pour les hommes. Chaque figure est un ensemble de nœuds avec des données. Les nœuds sont rangés de manière binaire selon certaines catégories.

La description textuelle suivante présente les données pour les femmes, suivies de celles pour les hommes. Chaque figure nécessite trois tableaux pour sa description textuelle.

Figure 2 – Femmes – Équivalent textuel tableau 1

Noeud	Étiquette et couleur de chaque noeud	Probabilité que les valeurs de l’IMC soient présentes	Probabilité que les valeurs de l’IMC soient manquantes	Pourcentage de l’échantillon	Catégorie dans laquelle le nœud peut être subdivisé	Nœuds qui suivent la subdivision pour « oui » et « non » respectivement
1	« présence » (en vert)	0.78	0.22	100 %	ORIGINE ETHNIQUE = non racisé	2, 3
2	« présence » (en vert)	0.8	0.2	70 %	S.O.	S.O.
3	« présence » (en vert)	0.73	0.27	30 %	HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.018	6, 7
6	« présence » (en vert)	0.74	0.26	29 %	S.O.	S.O.
7	« présence » (en vert)	0.57	0.43	1 %	ÂGE ≥ 15	14, 15
14	« présence » (en vert)	0.6	0.4	1 %	IMAGE DE SOI >24	28, 29
28	« présence » (en vert)	0.6	0.37	1 %	S.O.	S.O.
29	« absence » (en bleu)	0.21	0.79	0 %	S.O.	S.O.
15	« absence » (en bleu)	0.37	0.63	0 %	S.O.	S.O.

Le tableau suivant décrit les variables binaires de chacun des nœuds du tableau précédent. « Oui » signifie que le nœud inclut cette catégorie ; « non » indique l'autre catégorie restante. « S.O. » signifie que le nœud n'est pas atteint par cette catégorie en tant que nœud parent (par exemple, parce qu'il s'agit du nœud racine, ou parce qu’il est le nœud le plus éloigné du nœud racine, ou parce qu'il se trouve dans une autre région du modèle, etc.)

Figure 2 – Femmes – Équivalent textuel tableau 2

Noeud	ORIGINE ETHNIQUE = non racisé	HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.018	ÂGE ≥ 15	IMAGE DE SOI > 24
1	S.O.	S.O.	S.O.	S.O.
2	Oui	S.O.	S.O.	S.O.
3	Non	S.O.	S.O.	S.O.
6	Non	Oui	S.O.	S.O.
7	Non	Non	S.O.	S.O.
14	Non	Non	Oui	S.O.
28	Non	Non	Oui	Oui
29	Non	Non	Oui	Non
15	Non	Non	Oui	S.O.

Le tableau suivant décrit la distance entre chaque catégorie et le nœud racine. Par exemple, le nombre « 2 » signifierait que la catégorie est à deux branches du nœud racine (le nœud no. 1).

Figure 2 – Femmes – Équivalent textuel tableau 3

Nom de la catégorie (variable binaire)	Distance du nœud racine
ORIGINE ETHNIQUE = non racisé	1
HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.018	2
ÂGE ≥ 15	3
IMAGE DE SOI > 24	4

Figure 2 – Hommes – Équivalent textuel tableau 1

Noeud	Étiquette et couleur de chaque noeud	Probabilité que les valeurs de l’IMC soient présentes	Probabilité que les valeurs de l’IMC soient manquantes	Pourcentage de l’échantillon	Catégorie dans laquelle le nœud peut être subdivisé	Nœuds qui suivent la subdivision pour « oui » et « non » respectivement
1	« présence » (en vert)	0.78	0.22	100 %	SPORTS = oui, pratique sportive	2, 3
2	« présence » (en vert)	0.8	0.2	70 %	S.O.	S.O.
3	« présence » (en vert)	0.73	0.27	30 %	ECIG = oui, utilisation de la cigarette électronique	6, 7
6	« présence » (en vert)	0.8	0.2	10 %	S.O.	S.O.
7	« présence » (en vert)	0.7	0.3	26 %	HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.13	14, 15
14	« présence » (en vert)	0.71	0.29	24 %	S.O.	S.O.
15	« présence » (en vert)	0.54	0.46	2 %	LAIT ≥ 0.5	30, 31
30	« présence » (en vert)	0.58	0.42	2 %	IMAGE DE SOI > 17	60, 61
31	« absence » (en bleu)	0.39	0.61	0 %	S.O.	S.O.
60	« présence » (en vert)	0.6	0.4	1 %	VIANDE ≥ 1.5	120, 121
61	« présence » (en vert)	0.41	0.59	0 %	S.O.	S.O.
120	« présence » (en vert)	0.64	0.36	1 %	S.O.	S.O.
121	« présence » (en vert)	0.52	0.48	0 %	ORIGINE ETHNIQUE = non racisé	242, 243
242	« absence » (en bleu)	0.62	0.38	0 %	S.O.	S.O.
243	« absence » (en bleu)	0.33	0.67	0 %	S.O.	S.O.

Le tableau suivant décrit les variables binaires de chacun des nœuds du tableau précédent. « Oui » signifie que le nœud inclut cette catégorie ; « non » indique l'autre catégorie restante. « S.O. » signifie que le nœud n'est pas atteint par cette catégorie en tant que nœud parent (par exemple, parce qu'il s'agit du nœud racine, ou parce qu’il est le nœud le plus éloigné du nœud racine, ou parce qu'il se trouve dans une autre région du modèle, etc.).

Figure 2 – Hommes – Équivalent textuel tableau 2

Noeud	SPORTS = oui, pratique sportive	ECIG = oui, utilisation de la cigarette électronique	HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.13	LAIT ≥ 0.5	IMAGE DE SOI > 17	VIANDE ≥ 1.5	ORIGINE ETHNIQUE = non racisé
1	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
2	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
3	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
6	Non	Oui	S.O.	S.O.	S.O.	S.O.	S.O.
7	Non	Non	S.O.	S.O.	S.O.	S.O.	S.O.
14	Non	Non	Oui	S.O.	S.O.	S.O.	S.O.
15	Non	Non	Non	S.O.	S.O.	S.O.	S.O.
30	Non	Non	Non	Oui	S.O.	S.O.	S.O.
31	Non	Non	Non	Non	S.O.	S.O.	S.O.
60	Non	Non	Non	Oui	Oui	S.O.	S.O.
61	Non	Non	Non	Oui	Non	S.O.	S.O.
120	Non	Non	Non	Oui	Oui	Oui	S.O.
121	Non	Non	Non	Oui	Oui	Non	S.O.
242	Non	Non	Non	Oui	Oui	Oui	Oui
243	Non	Non	Non	Oui	Oui	Oui	Non

Le tableau suivant décrit la distance entre chaque catégorie et le nœud racine. Par exemple, le nombre « 2 » signifierait que la catégorie est à deux branches du nœud racine (le nœud no. 1).

Figure 2 – Hommes – Équivalent textuel tableau 3

Nom de la catégorie (variable binaire)	Distance du nœud racine
SPORTS = oui, pratique sportive	1
ECIG = oui, utilisation de la cigarette électronique	2
HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.13	3
LAIT ≥ 0.5	4
IMAGE DE SOI > 17	5
VIANDE ≥ 1.5	6
ORIGINE ETHNIQUE = non racisé	7

 

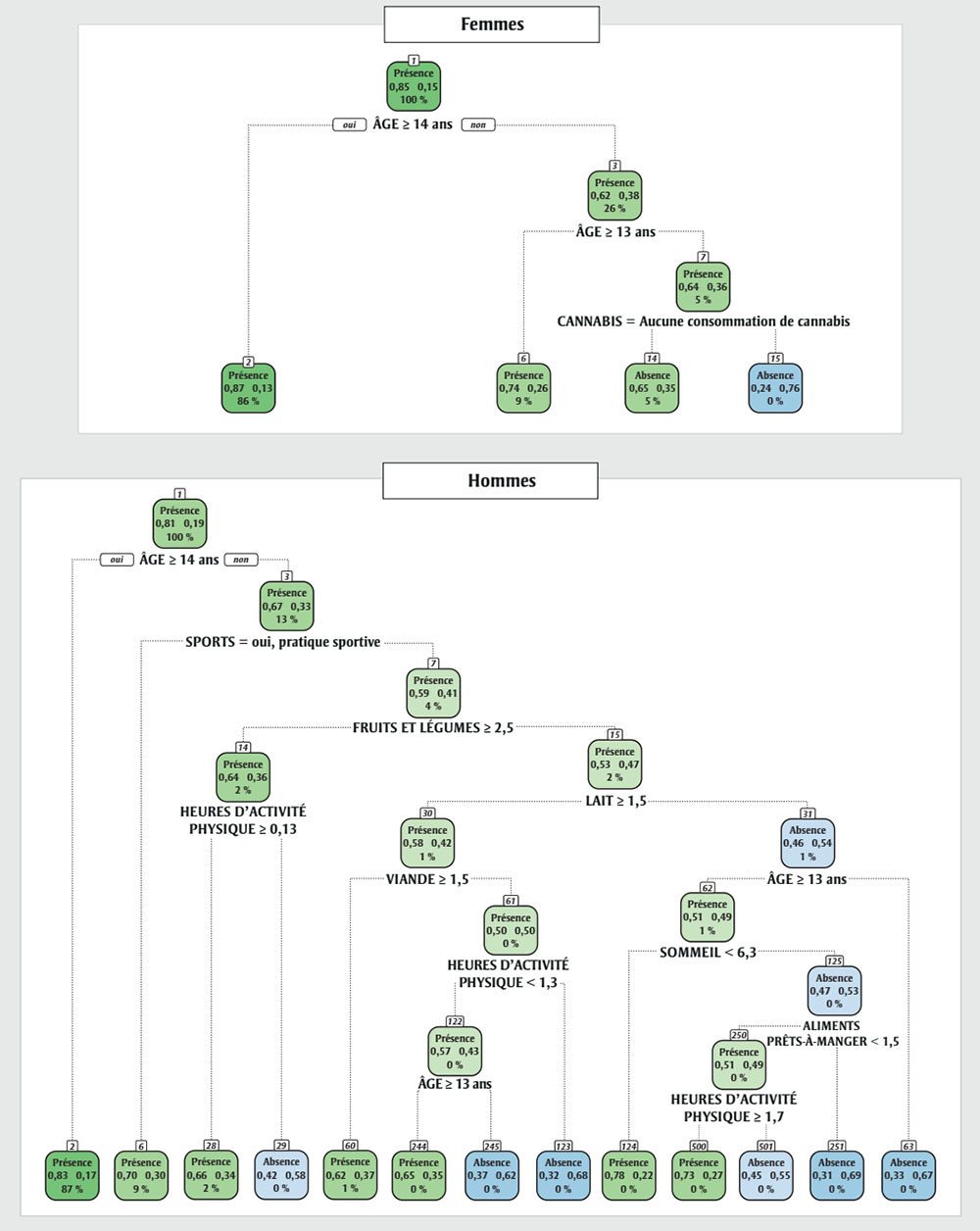
Figure 3 - Équivalent textuel

La figure 1 comprend deux figures plus petites : une pour les femmes et une pour les hommes. Chaque figure est un ensemble de nœuds avec des données. Les nœuds sont rangés de manière binaire selon certaines catégories.

La description textuelle suivante présente les données pour les femmes, suivies de celles pour les hommes. Chaque figure nécessite trois tableaux pour sa description textuelle.

Figure 3 – Femmes – Équivalent textuel tableau 1

Noeud	Étiquette et couleur de chaque noeud	Probabilité que les valeurs de l’IMC soient présentes	Probabilité que les valeurs de l’IMC soient manquantes	Pourcentage de l’échantillon	Catégorie dans laquelle le nœud peut être subdivisé	Nœuds qui suivent la subdivision pour « oui » et « non » respectivement
1	« présence » (en vert)	0.85	0.15	100 %	ÂGE ≥ 14	2, 3
2	« présence » (en vert)	0.87	0.13	86 %	S.O.	S.O.
3	« présence » (en vert)	0.62	0.38	26 %	ÂGE ≥ 13	6, 7
6	« présence » (en vert)	0.74	0.26	9 %	S.O.	S.O.
7	« présence » (en vert)	0.64	0.63	5 %	CANNABIS = pas de consommation de cannabis	14, 15
14	« présence » (en vert)	0.65	0.35	5 %	S.O.	S.O.
15	« absence » (en bleu)	0.24	0.76	0 %	S.O.	S.O.

Le tableau suivant décrit les variables binaires de chacun des nœuds du tableau précédent. « Oui » signifie que le nœud inclut cette catégorie ; « non » indique l'autre catégorie restante. « S.O. » signifie que le nœud n'est pas atteint par cette catégorie en tant que nœud parent (par exemple, parce qu'il s'agit du nœud racine, ou parce qu’il est le nœud le plus éloigné du nœud racine, ou parce qu'il se trouve dans une autre région du modèle, etc.).

Figure 3 – Femmes – Équivalent textuel tableau 2

Noeud	ÂGE ≥ 14	ÂGE ≥ 13	CANNABIS = pas de consommation de cannabis
1	S.O.	S.O.	S.O.
2	Oui	S.O.	S.O.
3	Non	S.O.	S.O.
6	Non	Oui	S.O.
7	Non	Non	S.O.
14	Non	Non	Oui
15	Non	Non	Non

Le tableau suivant décrit la distance entre chaque catégorie et le nœud racine. Par exemple, le nombre « 2 » signifierait que la catégorie est à deux branches du nœud racine (le nœud no. 1).

Figure 3 – Femmes – Équivalent textuel tableau 3

Nom de la catégorie (variable binaire)	Distance du nœud racine
ÂGE ≥ 14	1
ÂGE ≥ 13	2
CANNABIS = pas de consommation de cannabis	3

Figure 3 – Hommes – Équivalent textuel tableau 1

Noeud	Étiquette et couleur de chaque noeud	Probabilité que les valeurs de l’IMC soient présentes	Probabilité que les valeurs de l’IMC soient manquantes	Pourcentage de l’échantillon	Catégorie dans laquelle le nœud peut être subdivisé	Nœuds qui suivent la subdivision pour « oui » et « non » respectivement
1	« présence » (en vert)	0.81	0.19	100 %	ÂGE ≥ 14	2, 3
2	« présence » (en vert)	0.83	0.17	87 %	S.O.	S.O.
3	« présence » (en vert)	0.67	0.33	13 %	SPORTS = oui, pratique sportive	6, 7
6	« présence » (en vert)	0.7	0.3	9 %	S.O.	S.O.
7	« présence » (en vert)	0.59	0.41	4 %	FRUITS ET LÉGUMES ≥ 2.5	14, 15
14	« présence » (en vert)	0.64	0.36	2 %	HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.13	28, 29
15	« présence » (en vert)	0.53	0.47	2 %	LAIT ≥ 1.5	30, 31
28	« présence » (en vert)	0.66	0.34	2 %	S.O.	S.O.
29	« absence » (en bleu)	0.42	0.58	0 %	S.O.	S.O.
30	« présence » (en vert)	0.58	0.42	1 %	VIANDE ≥ 1.5	60, 61
31	« absence » (en bleu)	0.46	0.54	1 %	ÂGE ≥ 13	62, 63
60	« présence » (en vert)	0.62	0.37	1 %	S.O.	S.O.
61	« présence » (en vert)	0.5	0.5	0 %	HEURES D’ACTIVITÉ PHYSIQUE < 1.3	122, 123
122	« présence » (en vert)	0.57	0.43	0 %	ÂGE ≥ 13	244, 245
123	« absence » (en bleu)	0.36	0.68	0 %	S.O.	S.O.
244	« présence » (en vert)	0.65	0.35	0 %	S.O.	S.O.
245	« absence » (en bleu)	0.37	0.62	0 %	S.O.	S.O.
62	« présence » (en vert)	0.51	0.49	1 %	SOMMEIL < 6.3	124, 125
63	« absence » (en bleu)	0.33	0.67	0 %	S.O.	S.O.
124	« présence » (en vert)	0.78	0.22	0 %	S.O.	S.O.
125	« absence » (en bleu)	0.47	0.53	0 %	ALIMENTS PRÊTS-À-MANGER < 1.5	250, 251
250	« présence » (en vert)	0.51	0.49	0 %	HEURES D’ACTIVITÉ PHYSIQUE ≥ 1.7	500, 501
251	« absence » (en bleu)	0.31	0.69	0 %	S.O.	S.O.
500	« présence » (en vert)	0.73	0.27	0 %	S.O.	S.O.
501	« absence » (en bleu)	0.45	0.55	0 %	S.O.	S.O.

Le tableau suivant décrit les variables binaires de chacun des nœuds du tableau précédent. « Oui » signifie que le nœud inclut cette catégorie ; « non » indique l'autre catégorie restante. « S.O. » signifie que le nœud n'est pas atteint par cette catégorie en tant que nœud parent (par exemple, parce qu'il s'agit du nœud racine, ou parce qu’il est le nœud le plus éloigné du nœud racine, ou parce qu'il se trouve dans une autre région du modèle, etc.).

Figure 3 – Hommes – Équivalent textuel tableau 2

Noeud	ÂGE ≥ 14	SPORTS = oui, pratique sportive	FRUITS ET LÉGUMES ≥ 2.5	HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.13	LAIT ≥ 1.5	VIANDE ≥ 1.5	ÂGE ≥ 13	HEURES D’ACTIVITÉ PHYSIQUE < 1.3	ÂGE ≥ 13	SOMMEIL < 6.3	ALIMENTS PRÊTS-À-MANGER < 1.5	HEURES D’ACTIVITÉ PHYSIQUE ≥ 1.7
1	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
2	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
3	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
6	Non	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
7	Non	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
14	Non	Non	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
15	Non	Non	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
28	Non	Non	Oui	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
29	Non	Non	Oui	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
30	Non	Non	Non	S.O.	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
31	Non	Non	Non	S.O.	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
60	Non	Non	Non	S.O.	Oui	Oui	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
61	Non	Non	Non	S.O.	Oui	Non	S.O.	S.O.	S.O.	S.O.	S.O.	S.O.
122	Non	Non	Non	S.O.	Oui	Non	S.O.	Oui	S.O.	S.O.	S.O.	S.O.
123	Non	Non	Non	S.O.	Oui	Non	S.O.	Non	S.O.	S.O.	S.O.	S.O.
244	Non	Non	Non	S.O.	Oui	Non	S.O.	Oui	Oui	S.O.	S.O.	S.O.
245	Non	Non	Non	S.O.	Oui	Non	S.O.	Oui	Non	S.O.	S.O.	S.O.
62	Non	Non	Non	S.O.	Non	S.O.	S.O.	S.O.	Oui	S.O.	S.O.	S.O.
63	Non	Non	Non	S.O.	Non	S.O.	S.O.	S.O.	Non	S.O.	S.O.	S.O.
124	Non	Non	Non	S.O.	Non	S.O.	S.O.	S.O.	Oui	Oui	S.O.	S.O.
125	Non	Non	Non	S.O.	Non	S.O.	S.O.	S.O.	Oui	Non	S.O.	S.O.
250	Non	Non	Non	S.O.	Non	S.O.	S.O.	S.O.	Oui	Non	Oui	S.O.
251	Non	Non	Non	S.O.	Non	S.O.	S.O.	S.O.	Oui	Non	Non	S.O.
500	Non	Non	Non	S.O.	Non	S.O.	S.O.	S.O.	Oui	Non	Oui	Oui
501	Non	Non	Non	S.O.	Non	S.O.	S.O.	S.O.	Oui	Non	Oui	Non

Le tableau suivant décrit la distance entre chaque catégorie et le nœud racine. Par exemple, le nombre « 2 » signifierait que la catégorie est à deux branches du nœud racine (le nœud no. 1).

Figure 3 – Hommes – Équivalent textuel tableau 3

Nom de la catégorie (variable binaire)	Distance du nœud racine
ÂGE ≥ 14	1
SPORTS = oui, pratique sportive	2
FRUITS ET LÉGUMES ≥ 2.5	3
HEURES D’ACTIVITÉ PHYSIQUE ≥ 0.13	4
LAIT ≥ 1.5	4
VIANDE ≥ 1.5	5
ÂGE ≥ 13	5
HEURES D’ACTIVITÉ PHYSIQUE < 1.3	6
ÂGE ≥ 13	7
SOMMEIL < 6.3	6
ALIMENTS PRÊTS-À-MANGER < 1.5	7
HEURES D’ACTIVITÉ PHYSIQUE ≥ 1.7	8

Précision du modèle CART

Les tests de précision reposant sur la partition de test de l’ensemble de données ont indiqué que tous les modèles sont devenus plus précis après élagage. La précision de l’élagage des modèles CART sur l’IMC était de 69 % pour les filles et de 70 % pour les garçons, celle des modèles CART sur la masse corporelle était de 78 % pour les filles et de 80 % pour les garçons et celle des modèles CART sur la taille était de 85 % pour les filles et de 81 % pour les garçons.

Analyse

Cette étude a utilisé l’approche de l’arbre de décision pour analyser les données manquantes sur l’IMC, la taille et la masse corporelle dans un large échantillon de jeunes Canadiens. L’un des objectifs de cette étude était de fournir des informations sur la structure des données manquantes pour ces variables, car les données sur la taille et la masse corporelle autodéclarées par les jeunes sont parfois manquantes en grandes proportions et on manque d’analyses publiées sur ces données manquantes. L’autre objectif de cette étude était d’utiliser une méthode plus récente, celle des arbres de décision, pour analyser les données manquantes dans un ensemble de données afin de surmonter certains des obstacles des approches fondées sur la régression.

Lorsque nous avons précédemment étudié les données manquantes sur l’IMC, la taille et la masse corporelle dans cet échantillon à l’aide d’une approche de régression^{Note de bas de page 15}, nous avons constaté que nous avions besoin de plus d’informations sur la structure des données manquantes et sur la hiérarchie d’importance des variables. L’approche de l’arbre de décision utilisée ici a permis d’obtenir de l’information sur les mécanismes des données manquantes dans cet échantillon, ce qui peut être utile pour de futures études sur le surpoids et l’obésité chez les jeunes.

Mécanismes des données manquantes sur l’IMC, la taille et la masse corporelle

Dans les modèles CART sur les données manquantes que nous avons mis au point concernant l’IMC, l’âge et la perception du poids figurent parmi les premières partitions importantes pour les garçons et pour les filles. Des recherches antérieures ont fait l’hypothèse que les répondants plus jeunes étaient plus susceptibles d’omettre les valeurs de l’IMC parce qu’ils ne connaissaient ni leur taille ni leur masse corporelle^{Note de bas de page 26}, ce que semblent valider les modèles CART, car chaque partition par âge a conduit à un nœud où la probabilité de données manquantes était plus élevée dans le groupe de participants plus jeunes. La perception du poids a conduit à une division systématique entre ceux qui se percevaient en surpoids par rapport à ceux qui considéraient que leur poids était « à peu près juste » et « insuffisant », ce qui a entraîné une probabilité plus élevée de données manquantes dans le groupe qui se percevait en surpoids. Les études précédentes qui ont porté sur les mécanismes des données manquantes sur l’IMC n’ont pas utilisé de mesure de perception du poids, mais deux études ont révélé que plus les personnes étaient insatisfaites de leur poids, plus il était probable que les données sur leur IMC aient été manquantes^{Note de bas de page 14Note de bas de page 27}.

L’activité physique a également été l’une des premières partitions dans le modèle des filles et dans celui des garçons. Dans le modèle des filles, la musculation est un critère de partition important, avec des valeurs de l’IMC plus susceptibles d’être manquantes chez les répondantes qui ne faisaient pas de musculation. Un mécanisme similaire a été observé chez les garçons, mais à propos du sport et du nombre d’heures d’activité physique : le fait de ne pas faire de sport ou d’être, en moyenne, moins physiquement actif au quotidien crée des partitions où il est plus probable que les valeurs de l’IMC soient manquantes. Cela est conforme aux recherches précédentes utilisant des mesures de l’activité physique^{Note de bas de page 6Note de bas de page 7Note de bas de page 14}.

Des variables liées à la santé mentale sont également apparues dans le modèle des filles et dans celui des garçons. Chez les filles, c’est le bien-être et la santé mentale autoévaluée qui ont servi à la partition, et chez les garçons, c’est l’image de soi. Pour toutes ces variables liées à la santé mentale, des scores plus faibles (indiquant une santé mentale moins bonne) ont été associés à une plus grande probabilité de valeurs de l’IMC manquantes.

La partition constante des répondants se considérant en surpoids en un groupe à part où il était plus probable que des valeurs de l’IMC soient manquantes donne à penser que les répondants avec un IMC plus élevé étaient davantage susceptibles de ne pas le déclarer. Il est clair qu’on ne peut pas considérer la perception du poids comme une approximation directe de l’IMC ou de la masse corporelle, car les jeunes peuvent mal se classer^{Note de bas de page 28Note de bas de page 29Note de bas de page 30}, mais on peut considérer la perception du poids en parallèle avec d’autres facteurs pour déterminer quelle tendance sera la plus probable dans les données manquantes.

Les résultats liés à l’activité physique étayent l’idée selon laquelle les répondants qui n’ont pas fourni de données pour l’IMC sont plus susceptibles d’avoir un IMC plus élevé, car ceux qui sont moins physiquement actifs ont également été répartis dans des groupes où les valeurs de l’IMC étaient plus susceptibles d’être manquantes, et les associations inverses entre activité physique et IMC sont bien connues^{Note de bas de page 31Note de bas de page 32}. Ces résultats, et ce que nous savons des préoccupations accrues des adolescents quant à leur image corporelle^{Note de bas de page 33}, offrent la preuve que la désirabilité sociale peut jouer un rôle dans le fait que les jeunes de cet échantillon omettent de fournir leur taille et leur masse corporelle.

Les modèles CART sur la taille et la masse corporelle ont eu des critères de partition similaires à ceux des modèles sur l’IMC, l’âge étant une variable de partitionnement commune et l’activité physique, le régime alimentaire, la santé mentale et l’utilisation de substances étant des variables également présentes. Un résultat observable uniquement dans les modèles de données manquantes sur la masse corporelle porte sur l’origine ethnique : le modèle indique que les données sur la masse corporelle étaient plus susceptibles d’être manquantes chez les répondants « racisés ». Il est intéressant de noter que, bien que la perception du poids ait été identifiée comme variable clé des données manquantes sur l’IMC, elle n’a pas été considérée comme autant importante dans les modèles CART de données manquantes sur la masse corporelle, et ce, ni chez les garçons, ni chez les filles.

Utilité du modèle CART dans l’analyse des données manquantes sur l’IMC, la taille et la masse corporelle

L’approche de l’arbre de décision utilisée dans cette étude pour analyser les données manquantes présente plusieurs avantages par rapport aux approches de régression classiques. Étant de nature visuelle, les modèles d’arbre de décision sont particulièrement utiles pour comprendre comment les données manquantes peuvent être influencées par d’autres variables. Par exemple, l’inclusion et les directions du fractionnement liées à la perception du poids, à l’activité physique et à la santé mentale dans les modèles CART suggèrent que les données manquantes sur l’IMC ne sont peut-être pas manquantes aléatoirement, car elles apparaissent plus probables parmi les répondants ayant un IMC plus élevé. Bien que les données manquantes non aléatoirement ne soient pas un phénomène vérifiable, les modèles CART fournissent des preuves qui réfutent la présence d’un mécanisme de données manquantes complètement aléatoire, car nous avons identifié plusieurs sous‑groupes, sur la base des covariables observées^{Note de bas de page 34}, où les valeurs de l’IMC sont hautement susceptibles d’être manquantes. Les recherches futures sur le surpoids et l’obésité devraient tenir compte des mécanismes et du niveau de données manquantes sur l’IMC et, lorsque les analyses indiquent que les données pourraient être manquantes aléatoirement ou manquantes par omission prévisible, certaines approches statistiques (comme l’analyse des cas complets) risquent ne pas être idéales en raison du risque de biais^{Note de bas de page 9}.

Alors qu’un modèle de régression peut être autant efficace pour mettre en évidence les associations entre les variables prédictives et les données manquantes sur l’IMC (par exemple l’observation d’un rapport de cotes positif pour la perception d’être en surpoids), un des avantages des modèles CART est que la hiérarchie dans l’importance des variables est facile à visualiser. Dans le modèle CART sur l’IMC, le fait que la perception du poids figure parmi les deux premières partitions pour les garçons et pour les filles indique que cette variable est d’une importance primordiale dans la prédiction des données manquantes sur l’IMC. Nous avons précédemment étudié les données manquantes sur l’IMC à l’aide d’une régression^{Note de bas de page 15} : alors que la perception du poids était significativement associée aux données manquantes, elle ne constituait que l’une des nombreuses variables significatives et son importance relative était indiscernable de façon empirique.

Un autre avantage des modèles CART est que l’on peut suivre l’ordre de l’arbre de décision pour déterminer les sous-groupes importants. Par exemple, dans l’arbre sur les données manquantes sur l’IMC chez les garçons, il était plus probable que des valeurs de l’IMC soient manquantes pour les 9 % de l’échantillon qui ne pratiquaient pas de sport et se percevaient en surpoids. De plus, le fait de suivre des sous-groupes jusqu’au bas de l’arbre révèle que, dans l’ensemble, il est presque certain que les valeurs de l’IMC seront manquantes chez les répondants qui se perçoivent en surpoids et qui sont moins bien lotis en termes d’activité physique, de comportements alimentaires, de résultats scolaires et de santé mentale. Dit autrement : les modèles CART montrent que les répondants faisant partie de l’échantillon de cas complets (ceux ayant fourni toutes les données sur l’IMC) étaient physiquement, émotionnellement et mentalement plus sains que leurs homologues pour lesquels ces données étaient manquantes. À ce titre, une étude des données réalisée uniquement avec les cas complets risque fortement d’être biaisée, ce qui risque de conduire à des conclusions de recherche erronées et à des recommandations pour les politiques et les programmes connexes inappropriées.

L’analyse des données manquantes constitue souvent la première étape de certaines approches statistiques, par exemple de l’imputation multiple. Bien que de telles analyses soient nécessaires pour identifier des variables auxiliaires susceptibles de fournir des valeurs imputées raisonnables, la sélection de ces variables risque de se révéler difficile de nombreuses variables sont liées aux données manquantes. C’était le cas de nos travaux précédents utilisant la régression : presque toutes les variables étaient significativement associées à des données manquantes sur l’IMC, la taille et la masse corporelle, ce qui fait que la comparaison des tailles réelles n’aurait pas été appropriée, car ces variables utilisent différentes échelles^{Note de bas de page 15}.

La nature hiérarchique des modèles CART rend le processus de sélection des variables auxiliaires plus systématique. Par exemple, les modèles CART sont aptes à repérer les variables redondantes : alors que les travaux précédents de régression ont déterminé que l’objectif de poids était significativement lié aux données manquantes sur l’IMC^{Note de bas de page 15}, les modèles CART de cette étude n’ont pas fourni de partitions basées sur cette variable, peut-être parce que les données manquantes sur l’IMC sont suffisamment expliquées par la perception du poids uniquement.

Dans cette étude, nous avons fait la preuve de l’utilité du recours aux modèles CART pour analyser les données manquantes sur la taille, la masse corporelle et l’IMC chez les jeunes. Les données manquantes étant omniprésentes, une approche similaire est certainement utile dans de nombreux autres domaines de recherche appliquée. En outre, la disponibilité de progiciels d’apprentissage automatique dans R ainsi que la multitude de ressources en ligne rendent cette approche raisonnablement accessible et réalisable pour les chercheurs en sciences appliquées.

Conclusion

Cette étude enrichit la recherche, encore limitée, au sujet des données manquantes sur l’IMC, la taille et la masse corporelle chez les jeunes. Les modèles CART fournissent la preuve que l’âge, la perception d’être en surpoids, une activité physique plus faible et une santé mentale moins bonne conduisent à définir des sous-groupes où il est davantage probable que les valeurs de l’IMC soient manquantes. L’orientation du partitionnement du modèle pour ces variables suggère qu’il est davantage probable que les valeurs de l’IMC soient manquantes chez les jeunes ayant un IMC plus élevé, ce qui fait qu’une analyse supprimant les cas avec données manquantes mène probablement à des conclusions biaisées.

Des recherches futures utilisant des données autodéclarées par des jeunes pourraient considérer que les modèles CART sont un outil particulièrement utile pour analyser les données manquantes et facilitent le choix d’une approche statistique appropriée pour le traitement de ces données manquantes.

Remerciements

L’étude COMPASS a reçu le soutien d’une subvention transitoire de l’Institut de la nutrition, du métabolisme et du diabète des Instituts de recherche en santé du Canada (IRSC), grâce à l’attribution du financement prioritaire « Obesity-Interventions to Prevent or Treat » (Interventions pour prévenir ou traiter l’obésité) (OOP-110788; subvention accordée à SL), d’une subvention de fonctionnement de l’Institut de la santé publique et des populations (ISPP) des IRSC (MOP-114875; subvention accordée à SL), d’une subvention de projet des IRSC (PJT-148562; subvention accordée à SL), d’une subvention transitoire des IRSC (PJT-149092; subvention accordée à KP et SL), d’une subvention de projet des IRSC (PJT-159693; subvention accordée à KP); d’un accord de financement de la recherche conclu avec Santé Canada (n^o 1617-HQ-000012; contrat attribué à SL), et d’une subvention d’équipe des IRSC et du Centre canadien sur les dépendances et l’usage de substances (OF7 B1-PCPEGT 410-10-9633; subvention accordée à SL).

Une subvention pour les nouveaux chercheurs de la Fondation SickKids, en partenariat avec l’Institut du développement et de la santé des enfants et des jeunes des IRSC (subvention n^o NI21-1193, accordée à KAP), finance une étude à méthodes mixtes portant sur l’impact de la pandémie de COVID-19 sur la santé mentale des jeunes à partir des données de l’étude COMPASS. Le projet COMPASS-Québec bénéficie également d’un financement du ministère de la Santé et des Services sociaux du Québec et de la Direction régionale de santé publique du CIUSSS de la Capitale-Nationale.

Conflits d’intérêts

Les auteurs déclarent n’avoir aucun conflit d’intérêts.

Contributions des auteurs et avis

Conception : AD, AC, JPC et SL. Méthodologie : AD et AC. Analyse officielle et rédaction de la première version du manuscrit : AD. Acquisition de financement, ressources et supervision : SL Révision du manuscrit : AD, AC, JPC et SL. Tous les auteurs ont lu et accepté la version finale du manuscrit.

Le contenu de l’article et les points de vue qui y sont exprimés n’engagent que les auteurs; ils ne correspondent pas nécessairement à ceux du gouvernement du Canada.

Page précedente | Table des matières | Page suivante