Using machine learning algorithms to forecast disease surveillance in Ontario

 Download this article as a PDF
Download this article as a PDFPublished by: The Public Health Agency of Canada
Issue: Volume 46–6: Artificial intelligence in public health
Date published: June 4, 2020
ISSN: 1481-8531
Submit a manuscript
About CCDR
Browse
Volume 46–6, June 4, 2020: Artificial intelligence in public health
Implementation science
Good times bad times: Automated forecasting of seasonal cryptosporidiosis in Ontario using machine learning
Olaf Berke1, Lise Trotz-Williams1,2, Simon de Montigny3,4
Affiliations
1 Department of Population Medicine, Ontario Veterinary College, University of Guelph, Guelph, ON
2 Wellington-Dufferin Guelph Public Health, Guelph, ON
3 École de santé publique - Département de médecine sociale et préventive, Université de Montréal, Montréal, QC
4 Centre de recherche du CHU Sainte-Justine, Montréal, QC
Correspondence
Suggested citation
Berke O, Trotz-Williams L, de Montigny S. Good times bad times: Automated forecasting of seasonal cryptosporidiosis in Ontario using machine learning. Can Commun Dis Rep 2020;46(6):192–7. https://doi.org/10.14745/ccdr.v46i06a07
Keywords: disease surveillance, machine learning, statistical learning, cryptosporidiosis, artificial neural network, SARIMA, forecasting, seasonal time series
Abstract
Background: The rise of big data and related predictive modelling based on machine learning algorithms over the last two decades have provided new opportunities for disease surveillance and public health preparedness. Big data come with the promise of faster generation of and access to more precise information, potentially facilitating predictive precision in public health (“precision public health”). As an example, we considered forecasting of the future course of the monthly cryptosporidiosis incidence in Ontario.
Methods: The traditional statistical approach to forecasting is the seasonal autoregressive integrated moving-average (SARIMA) model. We applied SARIMA and an artificial neural network (ANN) approach, specifically a feed-forward neural network, to predict monthly cryptosporidiosis incidence in Ontario in 2017 using 2005–2016 data as a training set. Both forecasting approaches are automated to make them relevant in a disease surveillance context. We compared the resulting forecasts using the root mean squared error (RMSE) and mean absolute error (MAE) as measures of predictive accuracy.
Results: Cryptosporidiosis is a seasonal disease, which peaks in Ontario in late summer. In this study, the SARIMA model and ANN forecasting approaches captured the seasonal pattern of cryptosporidiosis well. Contrary to similar studies reported in the literature, the ANN forecasts of cryptosporidiosis were slightly less accurate than the SARIMA model forecasts.
Conclusion: The ANN and SARIMA approaches are suitable for automated forecasting of public health time series data from surveillance systems. Future studies should employ additional algorithms (e.g. random forests) and assess accuracy by using alternative diseases for case studies and conducting rigorous simulation studies. Difference between the forecasts from the machine learning algorithm, that is, the ANN, and the statistical learning model, that is, the SARIMA, should be considered with respect to philosophical differences between the two approaches.
Introduction
Cryptosporidiosis is a potentially lethal diarrheal disease that affects humans and animals. It is caused by the protozoan parasite Cryptosporidium spp.Footnote 1. Some 20 of the known 26 species have been associated with human infectionsFootnote 2. The majority of human infections are caused by C. hominis and C. parvum, which are mostly related to anthropogenic and zoonotic transmissions, respectivelyFootnote 3. The main infection route for humans is through consumption (including while swimming) of water contaminated with the parasites’ oocysts.
Cryptosporidiosis is often asymptomatic but can result in mild-to-severe gastrointestinal disease and even mortality. Human infection prevalence in North America ranges between 1% and 4% annually, but can be up to 20% elsewhereFootnote 4. While cryptosporidiosis is likely underreported, it is known to occur more frequently in children and immunocompromised people. No prophylactic treatment is available, making public health preparedness based on surveillance an important preventive option.
New opportunities for statistics, epidemiology and disease surveillance in public health have emerged over the last two decades since the advent of big dataFootnote 5Footnote 6. Eysenbach introduced the term “infodemiology” for the use of big data (and specifically social media use and behaviour data) in health surveillanceFootnote 7. A prominent example of infodemiology is the Google Flu Trends project, which predicted regional outbreaks of influenza 7 to 10 days ahead of conventional surveillance methods by the Center for Disease Control and Prevention (CDC) but was grossly overestimating influenza prevalenceFootnote 8. That project is a valuable example of the opportunities as well as the risks of big data, termed “big data hubris”Footnote 8Footnote 9.
Big data are often characterized by the five V’s: volume, variety, velocity, veracity and valueFootnote 9. Big data hubris refers to the veracity or truthfulness of the data. The promise of big data is that vast amounts of data (volume) of different types and from different sources (variety) provide a more complete and precise representation of reality, hence leading to “precision public health”Footnote 10. However, when the data are not representative of the population of interest, predictive inferences are biased.
Disease surveillance results in a big data situation due to data velocity and volume: data are constantly updated and growing in size. The dynamic nature of disease surveillance data requires an automated approach to analysis and forecasting. The traditional statistical time series modelling approach is the seasonal autoregressive integrated moving-average model (SARIMA) proposed by Box and JenkinsFootnote 11. A widely used machine learning algorithm for time series forecasting is the (feed-forward) artificial neural network (ANN)Footnote 12. We applied both forecasting approaches to predict monthly cryptosporidiosis incidence in Ontario in 2017 using 2005–2016 data as a training set. We compared these forecasting approaches using the 2017 incidence as test data, with the root mean squared prediction error (RMSE) and the mean absolute prediction error (MAE) as measures of accuracy.
Similar comparisons have been reported in the literature. Zhang and QiFootnote 13 compared SARIMA and ANN using simulations and showed that the ANN is consistently better at forecasting than the SARIMA model, when data are appropriately preprocessed. Kane et al.Footnote 14 compared forecasts of avian influenza H5N1 outbreaks by the SARIMA model to those from the random forest algorithm and concluded that machine learning provides enhanced predictive ability over the time series modelling. Similarly, in a study of typhoid fever incidence in China, Zhang et al. compared SARIMA modelling to three different ANN architectures; the researchers concluded that all three neural network algorithms outperform the statistical modelFootnote 15.
The goal of this study is to compare the two approaches to automating forecasting of monthly incidence rates of cryptosporidiosis in Ontario for the year 2017. The specific objectives wereFootnote 1 to compare the accuracy of forecasts using the RMSE;Footnote 2 to compare forecasts using the MAE; andFootnote 3 to visually compare the forecasted incidence rates to the observed time series.
Methods
The data we used were monthly incidence counts of cryptosporidiosis in Ontario for the years 2005 to 2017 as reported to Public Health Ontario and available from the respective homepagesFootnote 16. For analysis, we split the dataset into training data (monthly incidences in 2005 to 2016) and test data (monthly incidences in 2017).
For exploration purposes, we reported ranges of annual and monthly mean incidence in the training data and inspected the data with the seasonal and trend decomposition using Loess (STL) methodFootnote 17. The seasonal component was assumed to be time invariant or periodic, while the trend component was found using a moving window of length 73 months, or six years plus one month.
A SARIMA modelFootnote 11 is a data-generating model that includes seasonal and trend components. It is used to describe autocorrelations within a time series and to predict future values. It is described by the order of filters applied to remove seasonal and trend components as well as by the order of lagged correlations in the filtered series. The filtered series is assumed to be stationary and Gaussian. A brief description of the SARIMA model is: SARIMA(p,d,q)(P,D,Q)S, where S denotes the length of the season (here 12 months), d and D denote nonseasonal and seasonal difference filters to remove trend and seasonal components, respectively. Furthermore, p and P are orders of the nonseasonal and seasonal autocorrelation parameters, respectively. Finally, q and Q denote the nonseasonal and seasonal order of moving-average parameters. The SARIMA modelling approach was automated by using maximum likelihood estimation and stepwise backward model selection with the Bayesian information criterion (BIC). The SARIMA model as fit to the 2005–2016 training data was then used to forecast monthly incidences for 2017 test data.
The ANN is a data-driven and automated algorithm to forecasting time series data. While a variety of ANN architectures existFootnote 18Footnote 19, we applied the staple feed-forward multilayer neural network with a single hidden layer in this studyFootnote 12. More specifically, the ANN is described as ANN(p,P,k)S, where p, P and S have the same meanings as in the SARIMA model, and k denotes the number of nodes in the hidden layer. Automatic selection of the ANN’s order values was as follows: S=12 is known; k was the rounded value of (p+P+1)/2, where P was set to P=1 to accommodate linear seasonality; and p was selected as the optimal order of an autoregressive model fit to the remainder of term of the STL decomposed series.
We applied the ANN algorithm as follows: linear combinations of input data were subjected to the nonlinear sigmoid activation function 1/(1+exp(−z)) as output from a hidden layer, and the output from the hidden layer was then aggregated in the form of linear combinations, which resulted in the final output. The ANN was trained using 100 repetitions, that is, 100 different random starting values for the weight parameters of the linear combinations between input and hidden layer as well as the hidden and output layers. Furthermore, the input series (i.e. the 2005–2016 data) was preprocessed using an automatic selection of the Box–Cox transformation parameter (by the Guerrero methodFootnote 12) followed by studentizing (i.e. centring and scaling). For each repetition, the algorithm was trained by an iterative experimental process of optimizing a loss function. The resulting set of forecasts, or ensemble, was averaged over all iterations.
Both forecasting approaches provide prediction intervals. The SARIMA prediction interval was based on estimated model parameter. The ANN prediction interval was based on 1,000 bootstrapped sample pathsFootnote 12, that is, using resampled past residuals. In addition, both forecasting approaches were compared by their accuracy measures (RMSE and MAE) for the monthly forecasts and the observed test data of the year 2017.
All data analysis was performed in RFootnote 20 and RStudioFootnote 21 using the “forecast” packageFootnote 12.
Results
The time series of monthly reported cryptosporidiosis incidences in Ontario for the years 2005 to 2016 is dominated by a seasonal component, with summer peaks and only a weak – if any – upward trend (Figure 1). The STL decomposition in Figure 2 confirms this impression. The training data time series is relatively short with 12 years comprising 4,152 cases, or an annual average of 346 cases, which is equivalent to about 2.57 annual cases per 100,000 population at risk. The average number of monthly cases was 29, ranging from 6 to 109 cases over 2005 to 2016.
Figure 1: Time series plot of the monthly incidence of cryptosporidiosis in Ontario during the years 2005 to 2016
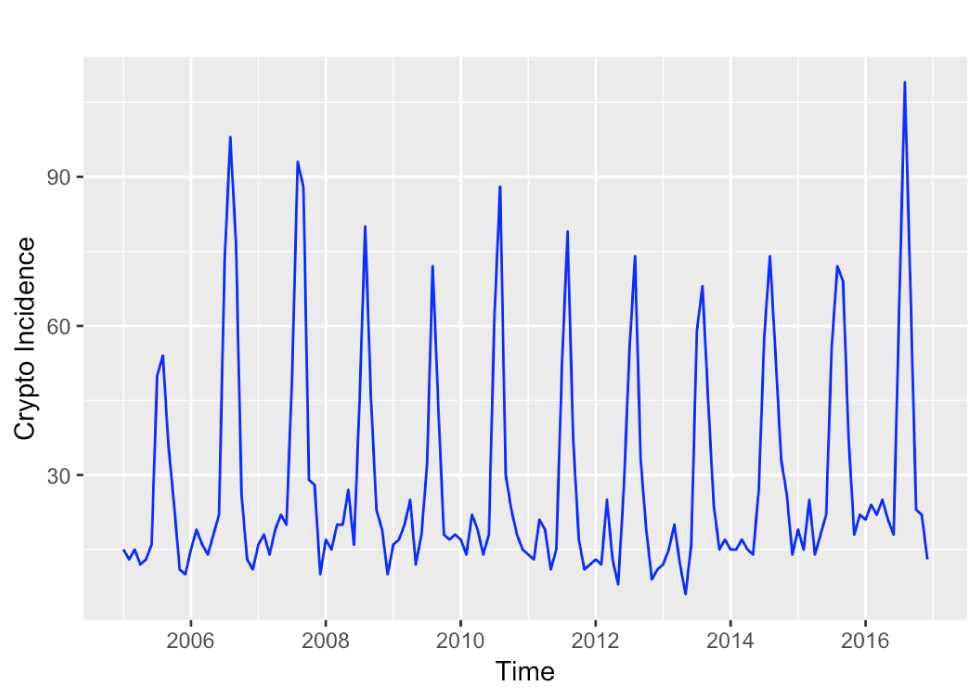
Text description: Figure 1
Figure 1: Time series plot of the monthly incidence of cryptosporidiosis in Ontario during the years 2005 to 2016
Time series plot of the monthly incidence of cryptosporidiosis in Ontario during the years 2005 to 2016. The incidence varies around 10 to 20 cases per month with no obvious time trend, but a strong seasonal increase to about 70 to 90 cases per month.
Figure 2: The cryptosporidiosis time series of monthly incidences from 2005 to 2016Figure 2 footnote a

Text description: Figure 2
Figure 2: The cryptosporidiosis time series of monthly incidences from 2005 to 2016Figure 2 footnote a
The cryptosporidiosis time series of monthly incidences from 2005 to 2016. This figure shows the time series together with its seasonal and trend decomposition using the Loess (STL) method. The figure combines 4 time series plots arranged in rows so that the time axes are aligned for comparison. The top plot shows the observed time series of incident cryptosporidiosis cases. This is followed by plots for the trend, seasonal and remainder components resulting form the STL decomposition.
The trend component is relatively flat ranging mainly between 25 and 30 cases per month, with a slight increase over the last four years to about 35 cases per month.
The seasonal component is the main characteristic and represents the largest proportion in the variability of the time series. The seasonal pattern is dominated by a large increase in cases during later summer, when cases counts increase from a level around −10 cases to about + 50 cases per month.
The remainder component varies roughly between −20 and +20 cases per month. It shows no obvious pattern; it appears to be random variation.
The stepwise automated model selection resulted in a SARIMA(1,0,0)(1,1,0)12 model with model parameter estimates being first order autoregressive parameter AR(1)=0.41 (standard error [SE]=0.08) and first order seasonal autoregressive parameter SAR(1)=−0.35 (SE=0.10) (Figure 3).
Figure 3: Forecasts for 2017 monthly cryptosporidiosis incidences with 80% and 95% prediction intervals from a SARIMA(1,0,0)(1,1,0)12 model

Text description: Figure 3
Figure 3: Forecasts for 2017 monthly cryptosporidiosis incidences with 80% and 95% prediction intervals from a SARIMA(1,0,0)(1,1,0)12 model
Forecasts for 2017 monthly cryptosporidiosis incidences with 80% and 95% prediction intervals from a SARIMA(1,0,0)(1,1,0)12 model. The forecast for 2017 captures the seasonal pattern well. The 95% prediction interval is wide and reaching into the negative for the last month, that is December 2017.
The automatically selected ANN is of order ANN(11,1,6)12, that is, the last 11 observations plus the first seasonal observation are linearly combined into six nodes of a single hidden layer. The input series was Box–Cox transformed with an automatically chosen parameter λ=−0.21. The forecasts from the ANN are visualized together with 80% and 95% prediction intervals in Figure 4.
Figure 4: Forecasts for 2017 monthly cryptosporidiosis incidences with bootstrapped 80% and 95% prediction intervals from an ANN(11,1,6)12

Text description: Figure 4
Figure 4: Forecasts for 2017 monthly cryptosporidiosis incidences with bootstrapped 80% and 95% prediction intervals from an ANN(11,1,6)12
Forecasts for 2017 monthly cryptosporidiosis incidences with bootstrapped 80% and 95% prediction intervals from an ANN(11,1,6)12. The forecast for 2017 captures the seasonal pattern well. The prediction interval is very narrow around the forecasted incidence and always positive.
The observed monthly incidences and rounded forecasts are presented in Table 1 and Figure 5 for both models. Table 2 shows the summaries of the RMSE and MAE from the 2017 forecasts for both approaches.
| Incidence rate per month | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Month | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
| Observed | 23 | 17 | 25 | 22 | 16 | 24 | 48 | 70 | 55 | 32 | 33 | 20 |
| SARIMA | 18 | 20 | 23 | 21 | 20 | 19 | 61 | 96 | 68 | 28 | 21 | 16 |
| ANN | 20 | 19 | 25 | 24 | 18 | 20 | 62 | 95 | 42 | 22 | 15 | 12 |
Figure 5: Time series plot of the observed monthly cryptosporidiosis incidences for 2017 and the forecasts from SARIMA and ANN approaches

Text description: Figure 5
Figure 5: Time series plot of the observed monthly cryptosporidiosis incidences for 2017 and the forecasts from SARIMA and ANN approaches
Time series plot of the observed monthly cryptosporidiosis incidences for 2017 and the forecasts from SARIMA and ANN approaches. The forecasts from both methods are very accurate for the first six months, and over-predict the seasonal peak in August of 2017. With increasing forecast horizon, the predictions are less accurate for the remainder of the year.
| Model | RMSE | MAE |
|---|---|---|
| SARIMA(1,0,0)(1,1,0)12 | 10.3 | 7.7 |
| ANN(11,1,6)12 | 11.2 | 8.4 |
Discussion
The monthly cryptosporidiosis incidence in Ontario is characterized by a dominant seasonal pattern that generally peaks in August. The short peak in incidence may support the concept of human behaviour as a main driver for infection since environmental conditions (e.g. ambient temperature) do not vary in a pattern similar to the incidence. No increasing trend was identified, meaning that the incidence is not emerging.
Neither the machine learning algorithm (i.e. the ANN) nor the statistical learning method (i.e. SARIMA) were found to have a superior performance in predicting monthly cryptosporidiosis incidence. While the ANN forecasts were closer to the observations for six months, the SARIMA performed better for a different group of five months; both methods were tied for the month of September of 2017 (see Table 1). However, the accuracy measures RMSE and MAE indicate a slight advantage for the SARIMA forecasts: the ANN’s RMSE and MAE were higher by 0.9 and 0.7 units, respectively (see Table 2).
This slight advantage for the SARIMA is interpreted as follows: the SARIMA forecasts are, on average, almost one case per month more accurate than ANN forecasts. Although this result is unexpected with respect to the cited reportsFootnote 13Footnote 14Footnote 15, it is in line with a systematic reviewFootnote 22 that found no evidence for more accurate predictions from machine learning alternatives to statistical logistic regression modelling. However, it should be noted that this is a case study and results are specific to this example. While the SARIMA model assumes white noise residuals and an additive seasonal component, this was not checked here using the automated modelling approach. Similarly, the ANN is optimized using backpropagation, which is known to have difficulties finding the optimal parameter estimatesFootnote 19. Therefore, the ANN employs ensemble forecasting to guard against individual erroneous forecasts.
Proper data preprocessing is important for machine learning algorithmsFootnote 23. This means a time series needs to be scaled and centred (i.e. studentized or normalized) prior to analysis. Data preprocessing is a natural part of the autoregressive integrated moving-average modelling approach, as trend and seasonal effects are filtered out before the model is fitted to the time series. In our study, stepwise model selection led to filtering out a seasonal effect, but a trend effect was neither identified nor removed. The ANN was preprocessed by a Box–Cox transformation, followed by centring and scaling.
Big data analysis is often presented together with machine learning algorithms for inference, that is, predictive modelling. The reason for doing so might originate from the impression that traditional statistical methods are inappropriate for the challenges of big data. For example, the variety of data expressed by the number of covariates could render traditional statistical inference less attractive and impractical. On the other hand, machine learning algorithms are designed around modern statistical methods for dimension reduction and regularization (e.g. Lasso regression). The training of machine learning algorithms is what is otherwise known as parameter estimation in statistical modelling and is no different from statistical learning methods, being based on cross-validation and bootstrapping.
In summary, to a certain degree statistical learning and machine learning do not differ. However, in public health, applications of big data analysis, namely predictive modelling including time series forecasting, differ from traditional biostatistical data analysis in terms of risk factor identification and assessment. Breiman distinguished this as “the two cultures” of statistical modelling: the data modelling culture and the algorithmic modelling cultureFootnote 24. He argued that statistical theory is irrelevant if modelling assumptions are not met in real-data situations. However, he also admitted that machine learning algorithms are often based on little theory, and modelling assumptions are replaced by properties of the algorithms, that is, whether these converge and deliver good predictions.
From a philosophical point of view, machine learning is based on a “black box” that is not open to interpretations or explanations. In the current example, the ANN(11,1,6)12 algorithm included a nonlinear combination of the time series data and 85 parametersFootnote 23. On the other hand, the SARIMA model describes how past observations affect the future course of a process; this characteristic might propose causal hypothesesFootnote 25. Therefore, it is not entirely correct to simply compare the forecasting methods by their predicted values or accuracy measures as the approaches are philosophically different and not entirely comparable: the ANN is a predictive algorithm, while the SARIMA is a descriptive and predictive model.
Limitations
A limitation of this study is the lack of adjustment for the population at risk. Indeed the Ontario population is steadily increasing, but at an annual rate below 0.5%, which is negligible in this context, where underreporting is of greater concern. No trend in the monthly cryptosporidiosis incidence rates was indicated by either the SARIMA or ANN approaches.
Conclusion
Cryptosporidiosis is a strongly seasonal disease, leading to good times and bad times of varying caseloads for public health. Machine learning methods suitable for forecasting of public health time series data from surveillance systems are becoming more popular; they have been demonstrated to be more accurate than traditional statistical methods. However, in this particular case study, the SARIMA model resulted in slightly lower RMSE and MAE and thus greater accuracy than the ANN. Both forecasting approaches captured the seasonal pattern of cryptosporidiosis well.
Future studies should employ additional algorithms (e.g. random forests) and assess accuracy in different setting, either by using alternative diseases for case studies or employing a more systematic approach and conducting simulation studies.
Authors’ statement
- OB conceived the study, collected the data and performed the data analysis
- OB, LTW and SDM all wrote and approved the manuscript
Conflict of interest
The authors declare having no conflict of interest.
Page details
- Date modified:
